No.223 矩形面积

给你 二维 平面上两个 由直线构成的 矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其 左下 顶点和 右上 顶点坐标表示：

示例 1：

输入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出：45

示例 2：

输入：ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出：16

提示：

• -104 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 104

思路分析

首先可以想想，两个长方形重叠有哪些情况，有如上图这样，也有这样：

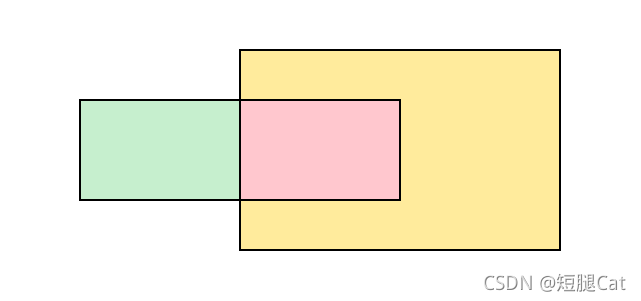
也有如下这样：

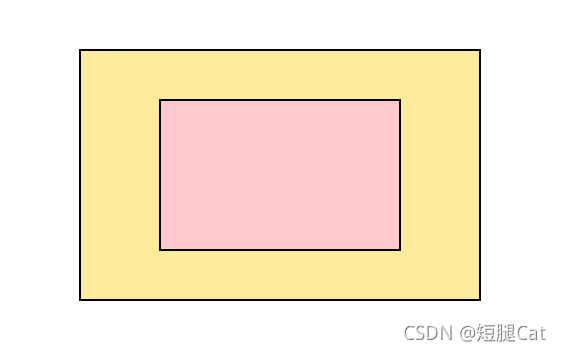
也有可能长这样：

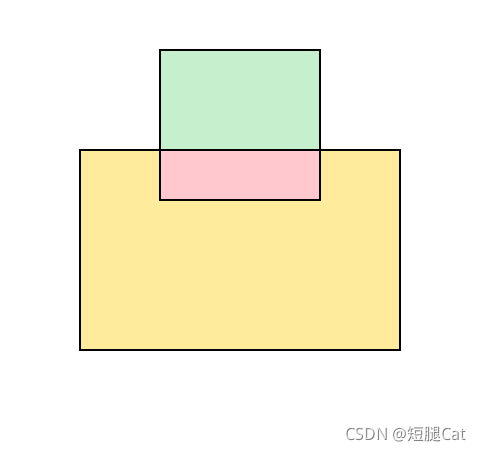
但其实不管他到底长什么样，我们都可以通过两正方形面积之和减去重合部分得出答案，设两长方形分别为 A 和 B，则：

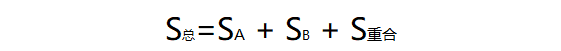
A 和 B 的面积很好求，这里就不再赘述，这里主要说说重合的面积如何求； 重合部分仔细考虑，他也是一个长方形，也有长和高，所以求出长和高是关键： 长为 x 轴方向某两个端点之差，高则是 y 轴方向某两个端点之差，那这两个点是哪两个呢？

是这两个点（这种情况是红色部分点减去绿色部分点，为正数）：

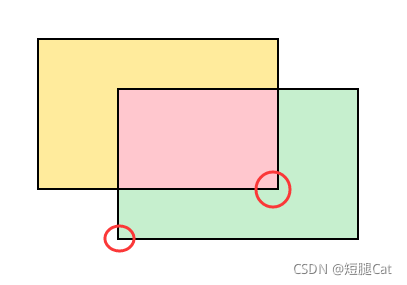
是这两个点（这种情况是绿色点减去黄色点，为负数）：

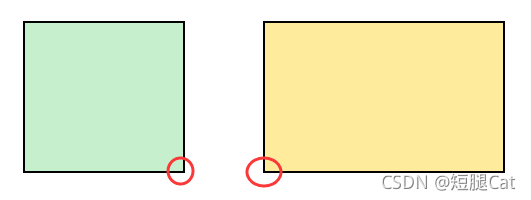
由此可见：两点分别为：两个长方形的最右边的 x 的最小值 & 两个长方形最左边的 x 的最大值

高度方向也类似，就不过于赘述。

若长或者高任一为负数 or0，则将其置为 0.得出的重合面积也为 0：

Java 代码

class Solution {
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int A = (ax1 - ax2) * (ay1 - ay2);
        int B = (bx1 - bx2) * (by1 - by2);
        int C_X = Math.max(0, Math.min(ax2 ,bx2) - Math.max(ax1, bx1));
        int C_Y = Math.max(0, Math.min(ay2 ,by2) - Math.max(ay1, by1));
        int C = C_X * C_Y;
        return A + B - C;
    }
}

Rust 代码

#![allow(unused)]
fn main() {
struct Solution;
pub fn compute(a: i32, b: i32, c: i32, d: i32) -> i32 {
    let t = c.max(a);
    (b - t).min(d - t).max(0)
}
impl Solution {
    pub fn compute_area(a: i32, b: i32, c: i32, d: i32, e: i32, f: i32, g: i32, h: i32) -> i32 {
        // 重叠面积
        let cd = compute(a, c, e, g) * compute(b, d, f, h);
        (c-a)*(d-b) + (h-f)*(g-e) - cd
    }
}
}