No.166 分数到小数
给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以 字符串形式返回小数 。
如果小数部分为循环小数,则将循环的部分括在括号内。
如果存在多个答案,只需返回 任意一个 。
对于所有给定的输入,保证 答案字符串的长度小于 104 。
示例 1:
输入:numerator = 1, denominator = 2 输出:"0.5"
示例 2:
输入:numerator = 2, denominator = 1 输出:"2"
示例 3:
输入:numerator = 2, denominator = 3 输出:"0.(6)"
示例 4:
输入:numerator = 4, denominator = 333 输出:"0.(012)"
示例 5:
输入:numerator = 1, denominator = 5 输出:"0.2"
提示:
-231 <= numerator, denominator <= 231 - 1denominator != 0
思路分析
这道题本质上就是要让我们用除法的思维去做题。
在我们做除法的时候,怎么判断重复循环的小数呢?
首先当然是进行预处理。包括以下几个步骤。
- 处理符号,将负号统一处理一下。因为两个正数相除显然比较符合人类的习惯。
- 将所有32位数字输入处理成64位,因为可能会超限。
- 处理整数部分,因为整数部分一般不参与到循环小数的范围内。
- 其他特殊情况。
在处理完上述步骤之后,我们得到了还是题目中的两个数字numerator和denominator。这两个数字仍然是被除数与除数的关系,只不过经过减去整数部分的处理之后,我们能确保numerator一定小于denominator。
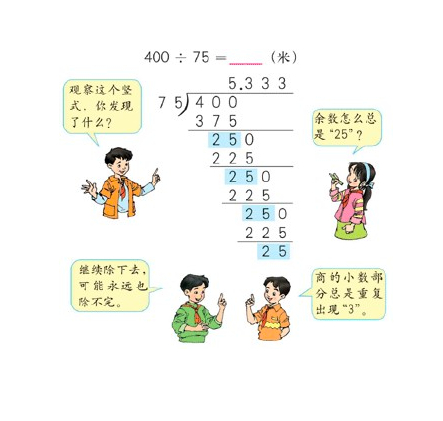
如果没有思路可以看一下上面这张图。这张图基本上概括了本题所需的循环小数部分的数学知识。 可以看出,在除法的过程中,遇到除不尽的数字,我们一般是采用余数的方式,并且继续拿余数乘10之后再除。可以确定的是,只有在余数出现相同的情况下,余数之后的情况也会一模一样,也就是说,第一次出现相同的余数就是循环节的位置。
在此处,我们使用一个哈希表来存之前出现过的所有余数,并且在第二次出现余数的时候,标注循环节的位置,结束程序。
Rust代码
#![allow(unused)] fn main() { struct Solution; use std::collections::HashMap; impl Solution { pub fn fraction_to_decimal(numerator: i32, denominator: i32) -> String { let mut ret = String::new(); if (numerator as i64 * denominator as i64) < 0 { ret.push('-'); } let mut denominator = (denominator as i64).abs(); let mut numerator = (numerator as i64).abs(); let pre = numerator / denominator; numerator %= denominator; let mut map: HashMap<i64, i32> = HashMap::new(); ret.push_str(&pre.to_string()); if numerator == 0 { return ret; } ret.push('.'); let mut ws = ret.len() as i32; loop { if numerator == 0 { break; } if map.contains_key(&numerator) { ret.insert(*map.get(&numerator).unwrap() as usize, '('); ret.push(')'); break; } map.insert(numerator, ws); numerator *= 10; ret.push((('0' as u8) + (numerator / denominator) as u8) as char); numerator %= denominator; ws += 1; } ret } } }